2021年4月18日 2021年7月14日

【超かんたん】ソートアルゴリズムとは？｜基本構造が分かる！

アルゴリズムとは「何らかの問題を解く手順」のことです。

アルゴリズムを習得することで、生活の視点が変わり、問題解決に役立てることができます。

プログラミングを行うにあたって入門的な存在の１つとして、ソートアルゴリズムが挙げられます。

この考え方は、プログラミングを行うにあたって不可欠なもの知識になってきます。

実際にアルゴリズムを学習しようと思っても、イメージが湧かず苦戦してしまう方も多いのではないでしょうか。

この記事では、このソートアルゴリズムについて、分かりやすく図解で説明していきますね。

-Contents-

ソートアルゴリズムとは？

ソートアルゴリズムは、ソート（整理、並べ替え）させるアルゴリズムです。

データベースをはじめ、プログラミングでは大量のデータを扱うことが多くあります。

その際に、データを昇順や降順など、一定の規則に従って整列させる際に必要になってくるアルゴリズムになります。

この記事は、ソートアルゴリズムについて分かり安くまとめていますので、どうぞお読みください！

ソートアルゴリズムの種類

ソートアルゴリズムにも、整列方法や計算方法によって多くの種類が存在します。

そのため、実際のプログラミングでは、最適なアルゴリズムを選択する必要があるのです。

これから、ソートアルゴリズムで代表的な下記のアルゴリズムについて、紹介してみますね。

バブルソート
クイックソート
マージソート
選択ソート
挿入ソート
ヒープソート

バブルソート（ソートアルゴリズム）

多くのソートアルゴリズムの中で、バブルソートは最も基本的なアルゴリズムかもしれません。

一言でいうと、隣接する値どうしの比較、入れ替えを繰り返すことで、値を大きい順または小さい順に整列させるアルゴリズムです。

隣の値と比較
左から小さい順に整列（左の値が大きければ交換する）
1,2を繰り返し行う

※右から小さい順に整列する場合は、逆に並べる

バブルとは「泡」のことで、値が泡のようにボコボコが浮かんでいくように見えるのが由来です。

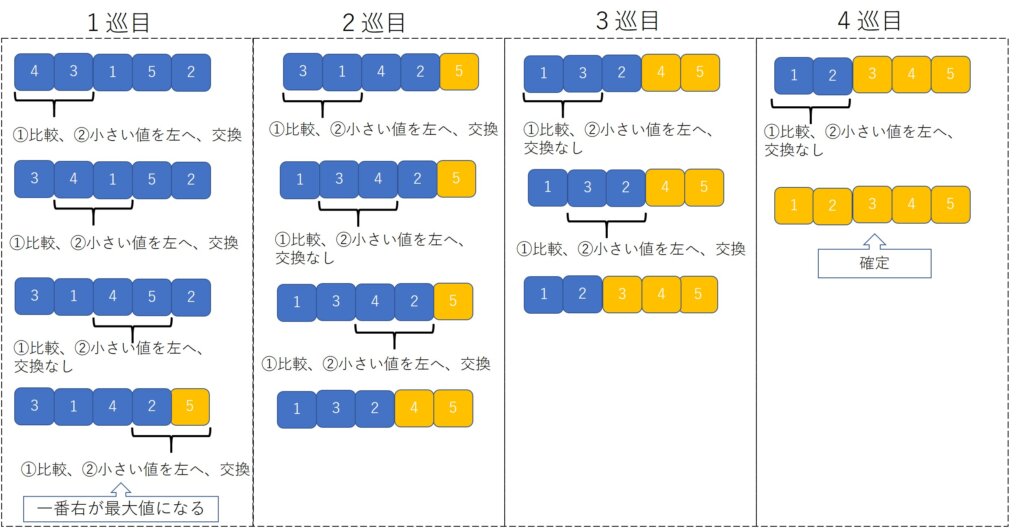
このように、隣り合う要素の大小を何度も比較しながら整列していくアルゴリズムになります。

バブルソートは、最もシンプルな考え方をしたアルゴリズムになります。

クイックソート（ソートアルゴリズム）

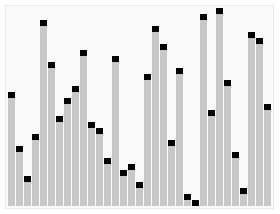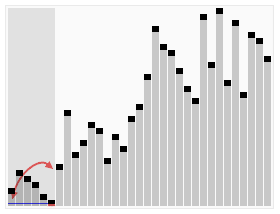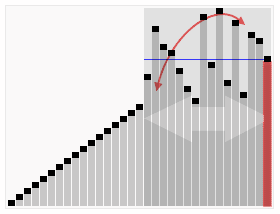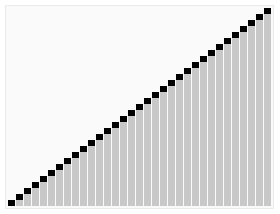
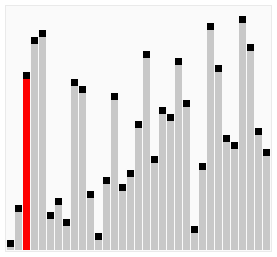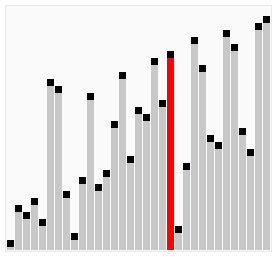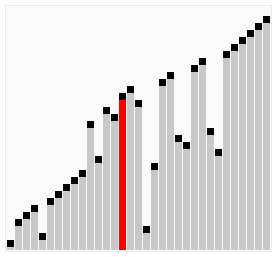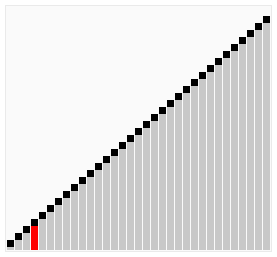
クイックソートは、ランダムなデータを整列するには、もっとも高速に実行できるアルゴリズムです。

クイックソートでは、データ比較や交換の回数を非常に少なくして、最も効率良く並べ替えます。

実際の手順としては、

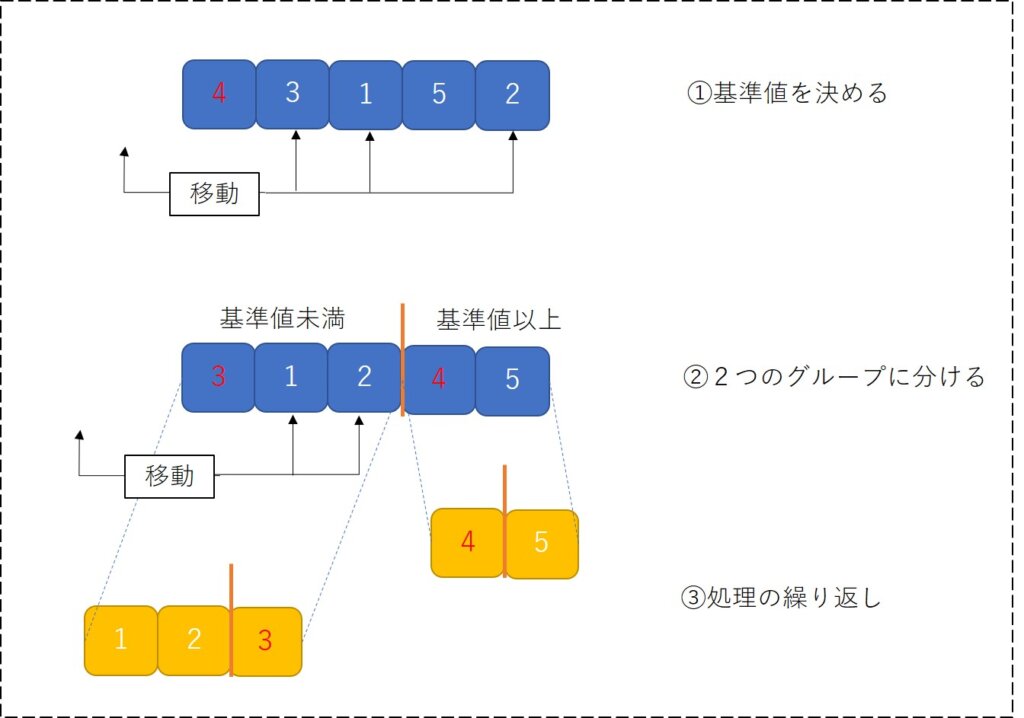
基準値（ピボット）を決める
データ群を基準値以上と基準未満の2つのグループに分ける（大・小２つのグループに分ける）
処理を繰り返す（①、②）ことで整列していく

基準値（ピボット）の決め方は条件で指定できますが、仮に「配列の左先頭の値」というルールにしてみると、次のようなに実施されます。

このように、クイックソートは「既にある程度並べられている」データでは効果が弱いというデメリットもありますが、ランダムなデータを整列する際は、高速なアルゴリズムになります。

マージソート（ソートアルゴリズム）

マージソートは、データを２分割し、列が1つの要素になるまで細分化した後、２つの列の併合（へいごう）を繰り返して配列していくアルゴリズムです。

2分割した値の要素数が1つになるまで、2分割を繰り返す
分割した要素同士を並び替えしながら戻していく

それでは具体的に、図解でマージソートの流れを説明していきます。

【手順1】
　2分割した値の要素数が1つになるまで、2分割を繰り返す

各要素数が一つになったので、ここで2分割の繰り返しは終了です。

【手順2】
　分割した要素を並び替えしながら戻していく

ここでポイントなのは、並び替えをすることです。

これで、マージソートでの整列は完了です。

このように、マージソートは、要素数が1になるまで2分割を繰り返し、整列しながら戻していく分割統治法に基づくアルゴリズムです。

選択ソート（ソートアルゴリズム）

選択ソートは、「先頭の値を対象データの中から、最小値を探し、先頭の値と交換する」作業を繰り返して整列していくアルゴリズムです。

先頭の値とデータの中の値を比較して、最小値を探し出す
先頭の値と最小値を交換する
交換した先頭の値は整列を確定させる
次の値を先頭の値として１～３の整列を繰返す
全ての値が確定されたら整列完了

上記の手順のように、１～３を繰返すことで整列することができます。

具体例を一つ見ていきたいと思います。

［１巡目］上記１～３

［２巡目］上記１～３

［３巡目］上記１～３

［４巡目］上記１～３

これで選択ソートでの整列完了になります。

このように、選択ソートは、データ内の最小値と先頭の値との交換を繰り返して、整列する整列アルゴリズムです。

挿入ソート（ソートアルゴリズム）

挿入ソートは、あらかじめ「整列された配列」の中に、適切な位置に値を挿入していくアルゴリズムです。

「整列された配列」がない状態でも、1つの値だけであれば「整列された配列」と考えられますね。

そのため、整列された配列がないときは、下記の1~3のような手順で行います。

「整列されていない配列（整列前）」から１つの値を取り出す
１で取り出した値を「配列された整列（整列後）」の適切な位置に挿入していく
1と2を繰り返し全ての値が「配列された整列」に挿入し終われば整列完了

具体例を一つ見ていきたいと思います。

【手順1】［挿入ソート］

「整列前」から”4″を取り出し、「整列後」に挿入します。

【手順2】［挿入ソート］

「整列前」から”3″を取り出し、「整列後」に挿入します。
“3”と”4″を比較し、”3″の方が小さいため、”4″の左側に挿入します。

【手順3】［挿入ソート］

「整列前」から”1″を取り出し、「整列後」に挿入します。
「整列後」の”3″と比較し、”1″ は “3”より小さいため、”3″の左側に挿入します。

【手順4】［挿入ソート］

「整列前」から”5″を取り出し、「整列後」に挿入します。
「整列後」の”1″と比較し、”5″は”1″より大きいため次へ
「整列後」の”3″と比較し、”5″は”3″より大きいため次へ
「整列後」の”4″と比較し、”5″は”4″より大きいため次へ
“5”は「整列後」の中で一番大きな値となりますので、適切な最後尾に追加します。

【手順5】［挿入ソート］

「整列前」から”2″を取り出し、「整列後」に挿入します。
「整列後」の”1″と比較し、”2″は”1″より大きいため次へ
「整列後」の”3″と比較し、”2″は”3″より小さいため、”3″の左側に挿入します。

整列前の要素を全て整列後に挿入できたので、これで挿入整列は完了になります。

このように、値を１つずつ適切な位置に挿入する整列していくアルゴリズムです。

ヒープソート（ソートアルゴリズム）

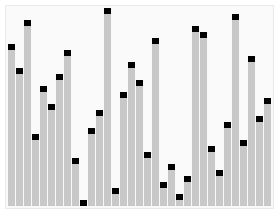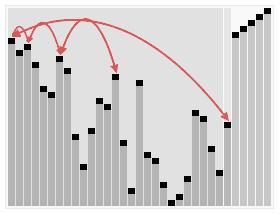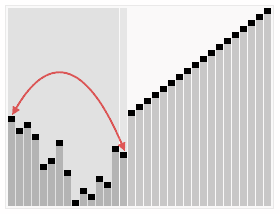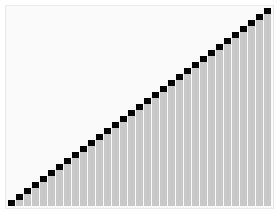
ヒープソートは、データを「完全二分木」といわれる木構造にして、それを根から葉のように、最大値または最小値を整列させるアルゴリズムです。

以下のような手順でソートするアルゴリズムです。

整列前の配列を木構造に構築する　※仮の位置
木構造の値が最大値または最小値になるように位置を入れ替える
全ての値を入れ替えたら、一番上の値は整列後データに追加する
1～3の手順を繰り返して、全ての値を整列する

【手順1】［ヒープソート］

整列前のデータを木構造にします。

【手順2】［ヒープソート］

下から順番に入れ替えを行い、木構造の根（ルート）が最大値になるようにします。

　【一番下の値（葉）から比較】

この木構造で一番根になる”3″と”5″と”2″を比較します。
3つの値では”5″が一番大きいので、”5″と”3″を入れ替えます。

　【１段上の値（葉）を比較】

次に一つ上のグループである”4″と”5″と”1″を比較します。
3つの値では”5″が一番大きいので、”5″と”4″を入れ替えます。

【手順3】［ヒープソート］

一番上の値は整列済みデータに追加する

一番上の値が最大値になりました。
整列後データに最大値の”5″を追加します。

【手順4】［ヒープソート］

　【木構造の再構築】

“5”を除いて、整列前の木構造を再構築します。

この時、一番下の段の最小値“2”を一番上に持ってきます。

　【値の比較・整列】

手順２・３と同様に、値を木構造の下から比較し並び替え、最大値を整列していきます。

この手順を繰り返して全ての値を整列します。

このように、ヒープソートは、データを木構造にして整列させるアルゴリズムです。

また、データの中から優先度の高いデータから順序通り取り出す仕組みは、様々なアプリケーションやアルゴリズムにも応用されています。

ソートアルゴリズムの学習法

プログラミングにおいて、アルゴリズムは欠かせません。

しかし、アルゴリズムと聞くだけで、数式の理屈を並べたもの･･･というイメージをもたれてしまって、学ぶことを拒絶されてしまっています。

そこで今回は、こちらの本をおススメします。

リンク

アルゴリズムが数式のような難しいものでなく、パズルのように楽しめるものということが分かっていただけると思います。

どうぞ、単純明快で分かりやすいので楽しく学習してみてください！

ちょっと試すだけでも未来は大きく広がりますよ。

まとめ（アルゴリズムのすすめ）

プログラミングの資質は「アルゴリズムへの理解度」です。

また、プログラミングにおいてソートアルゴリズムは非常に重要で頻繁に使われています。

的確なアルゴリズムを適用することで、大幅にパフォーマンスを向上することができます。

「スクラッチ（Scratch）」という言語では、遊ぶ感覚でプログラミングをしながらアルゴリズムを身に付けることができます。

こちらの本では、スクラッチ（Scratch）のはじめ方から学ぶことができます。

アルゴリズムを身に付ければ、びっくりするほど世界観が変わります！試しに学んでみませんか？

リンク

プログラミングに関わらない人も、アルゴリズムを学習することで、生活で抱えるあらゆる問題を効果的に対処することができるようになり、楽しく生活を送れるようになれます。

プログラミン的思考を身に付けるということは、アルゴリズムを身に付けることです。

こちらの記事で、最適なテキストを選ぶこともできます。

この記事を最後まで読んでくれて有難うございました！